Friday Science 3d: Principles of Quantum Mechanics

Sixth installment summarizing Susskind's, Quantum Mechanics: The Theoretical Minimum.

Chapter 1: Dirac was much smarter than I (introducing linear algebra).
Chapter 2: Quantum States (a.k.a., more linear algebra)
Chapter 3a: Linear Operators
Chapter 3b: Eigenvectors
Chapter 3c: Hermitians and Fundamental Theorem of QM

1. Again there is the sense that if I can just make it a little further, he'll connect this stream of math to something concrete so that all the rest will click. I feel like I'm reading 1 John.

Principle 1: Observable quantities in quantum mechanics are represented by linear operators. These have to be Hermitian as well.

Principle 2: The possible results of a measurement are the eigenvalues of the operator that relates to that observable. If a system is in the eigenstate ∣λ〉 , the result of a measurement has to be λ .

Principle 3: Distinguishable states are orthogonal vectors.

Principle 4: The probability of observing a value λ is 〈A∣λ〉² That is the probability of observing a particular eigenvalue is the square of the overlap between the eigenvalue and that state in general.

2. So Susskind uses the spin operator as an example. A spin operator provides information about the spin component in a specific direction. There is a spin operator for each direction in which the measuring apparatus can be oriented.

So he asks what an appropriate "spin operator" might be for the "up-down" aspect of spin. For up, the value will be one for up and zero for down. For down, the value will be zero for up and -1 for down. This corresponds to the following matrix:

z matrix (up down)

This satisfies the conditions: 1) it represents one component of the spin, 2) the possible results are +1 and -1. These are the eigenvalues of this matrix. 3) up and down are orthogonal.

3. He derives the matrices for the "right left" and "in out" components as well. These three matrices constitute the "Pauli matrices."

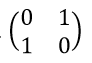x matrix (left-right)

y matrix (in out)