Friday Gen Eds MS7: The Basic Tools of Algebra

This is the seventh post in the math/science part of my "Gen Eds in a Nutshell" series. It's a series of ten subjects you might study in a general education or "liberal arts" core at a university or college. I've already done the subject of philosophy, and I'm over half way through the world history subject on Wednesdays. I'm combining the last two on math and science into one series on Fridays.

Thus far in the math/science subjects:

• Math/Science Overview
• Basic Types of Numbers
• The Atom and Quantum Physics
• The Periodic Table
• Molecules and Ions
• Chemical Reactions

______________________________
Solving for x
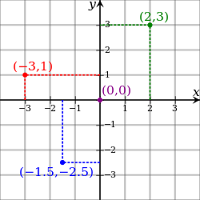
1. It is hard to convey how much math lept forward and the greatest developments in science became possible when algebra really began to develop in the late 1500s. Algebra is basically the use of letters to stand for unknown qualities that can change (called variables because they can vary in what number they stand for). For example, x + 6 = 10. If I need 10 apples and I already have 6, how many more do I need? [1]

But this area of math did not have its greatest impact until René Descartes (1596-1650) developed it, coming up with a way to graph equations (the "Cartesian coordinate system, to the right). It was Descartes who designated the x as the unknown it has come to be.

Algebraic equations are used to express real world situations using symbols. Simple unknowns, like the one above, are often easy enough for us to solve without using algebra. But algebra lets us express much more difficult situations, often with more than one unknown, and then to solve them.

2. Perhaps the first key to solving for x is knowing that 1) you can add or subtract any amount as long as you do it to both sides of the equation and 2) you can multiply or divide any amount as long as you do it to both sides of the equation.

So in the example above, x + 6 = 10, I can subtract 6 from both sides and the equation remains the same basic situation. So x + 6 - 6 = 10 - 6. I can simplify this to x = 4, and I have my answer.

As another example, let's say I have 33 dollars to spend and I want to bring as many friends as I can to a play where the tickets are 5 dollars a piece. I also have to pay 8 dollars for a taxi ride to get there. How many friends can I invite? I might express this situation by the equation 5x + 8 = 33.

First I subtract 8 from each side, giving me 5x = 25. Then I divide both sides by 5, giving me x=5. So I can bring 5 friends.

The very simple equations above could be expressed as a point on a number line, x = 5.

3. The equations above are "equalities." This equals that. There are also "inequalities." So x can be anything "greater than" 5: x > 5. And y can be anything "less than or equal to 6": y ≤ 6.

Another kind of equation is the "absolute value." The absolute value of a number is its positive value. For 5, it's easy. 5 is already positive. But for -5, it's absolute value is 5. The absolute value is usually written between two up and down lines.

Linear Equations
4. Sometimes there is more than one unknown. x + y = 10. An equation of this sort, where two variables (to the first power, as here) are in play, is called a linear equation because it graphs as a line. As the x changes, the y changes accordingly.

So let's say that you want to build a device that requires 6 of x for every 2 of y and costs $12. So we have an equation in two variables: 6x + 2y = 12. Or a simplified version would be 3x + y = 6.

A nice way to put the formula so it can be graphed is y = -3x + 6. This is the "slope-intercept" form or the y = mx + b form. B here tells us where this line hits the up and down line, usually called the y axis. So b is the "y-intercept." In this case, the line will cross the y axis at 6.

M is then the "slope," that is how the line "rises" for every bit the line goes to the right or left. So if the slope is -3, then the line goes down three units for every one unit that it goes to the right.

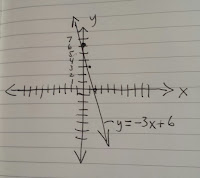To the right is what that graph would look like. The horizontal line is often called the x-axis. As I already said, the vertical line is often called the y-axis. So in this graph, the point 6 on the y axis is the y-intercept, where this line crosses the y-axis. Then the slope is negative three. The line goes down three (-3) for every 1 that x increases.

The slope is the "rise over the run," the amount it goes up or down for every one it goes right.

5. We locate points by using the format of (x, y), where x is the location of the point along the x-axis and y is the point along the y-axis. So the y-intercept is at (0, 6). If you look, the x-intercept (where it crosses the x axis) is at (2, 0). If you plug these numbers into the original formula, y = -3x + 6, you'll find that the numbers work. In fact, the line is all the sets of x's and y's that make the formula come out right. So (1, 3) works. (-1, 9) works. An infinite number of points work--the points on this line.

6. Sometimes you can have two equations that apply to a certain situation. Let's say you have 16 seats at a dinner, but for some reason you need to have 3 women for every one man. So f + m = 16 (the total number of women and men). At the same time, there are going to be three times as many women as men (f = 3m).

We can solve this situation in a couple of ways. For this one, substitution is the easiest. So we know that f = 3m, so we can plug this in for f in the other equation: (3m) + m = 16. So 4m = 16 and m = 4.

Now we can plug this value for 4 back into one of the original equations: f + 4 = 16, f = 12. So we should invite 12 women and 4 men. [2]

Quadratic Equations
7. There are equations where the variable is raised to a power more than 1. "Quadratic" equations are equations where the highest variable is squared. d = t² - 4t - 12. This is the kind of equation that would be in play if you were tracking the motion of a baseball you hit into left field.

So we solve an equation like this one by factoring it. So t² - 4t - 12 can be factored into (t - 6)(t + 2). We know this because if you multiply the material in these two parentheses together you get the other. The way you multiply something of this sort is by using the FOIL method (first, outside, inside, last).

So when does this equation work? For example, if t is time and d is the distance from the ground, then the baseball is at zero when t - 6 = 0 and when t + 2 = 0. The second one doesn't make sense because it is t = -2. But the second one makes sense t = 6. So the ball will return to the ground in six seconds.

8. Some quadratic equations are hard to factor. In such cases, the quadratic equation is used.

If you put a quadratic function into the form ax² + bx + c = 0, then a and b are coefficients in front of the variables. Plugging these into the formula tells you what x works.

Other Equations
9. Of course there can be equations of higher powers than these. There are cubic equations (raised to a third power). And there can be equations raised to even higher powers. These are "polynomial" equations, where the "poly" means powers more than one.

There are inverse functions (1/x). There are equations for circles, ellipses, hyperbolas. There are trigonometric functions (sine, cosine, tangent). We we will consider in our post on Geometry and Trigonometry yet to come.  

Next Week: Math/Science 8: Thermodynamics

[1] A Greek named Diophantus (200s AD) has often been called the father of algebra, but the name "algebra" comes from the medieval Persian al-Khwarizmi (ca. 780-850).

[2] You could also find the solution by graphing both of these line equations and then finding the intersection point on a graph. In this case, the intersection would be (12, 4), if the we were graphing points as (m, f).